Tan^2 identities 105376-Tan 2 identities

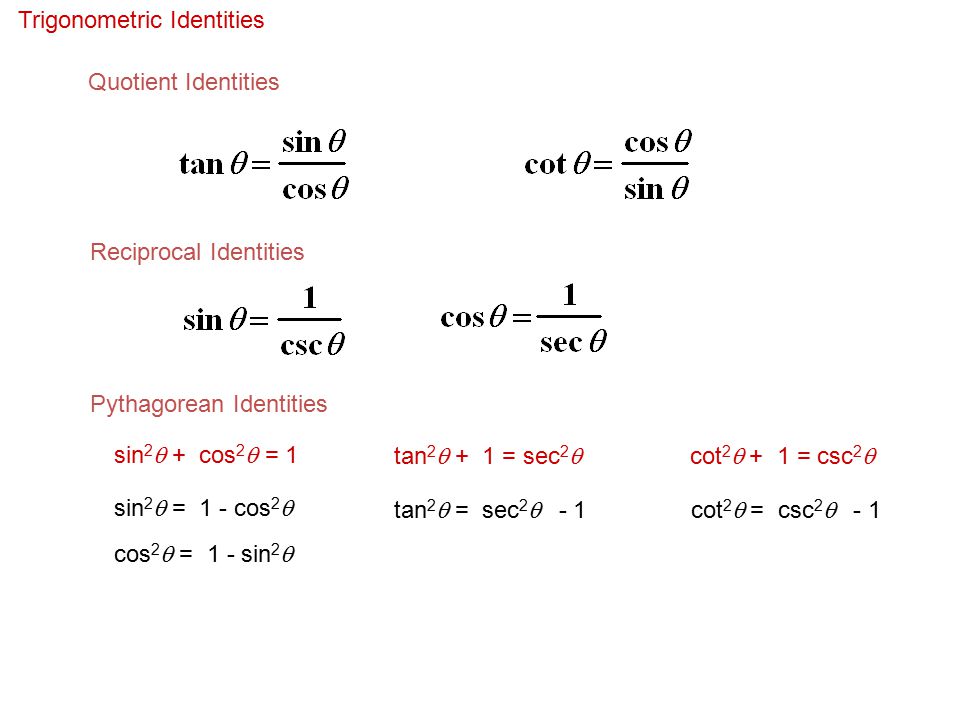
Reciprocal identities sinu= 1 cscu cosu= 1 secu tanu= 1 cotu cotu= 1 tanu cscu= 1 sinu secu= 1 cosu Pythagorean Identities sin 2ucos u= 1 1tan2 u= sec2 u 1cot2 u= csc2 u Quotient Identities tanu= sinu cosu cotu= cosu sinu CoFunction Identities sin(ˇ 2 u) = cosu cos(ˇ 2 u) = sinu tan(ˇ 2 u) = cotu cot(ˇ 2 u) = tanu csc(ˇ 2 u) = secu secIf the angles are doubled, then the trigonometric identities for sin, cos and tan are sin 2θ = 2 sinθ cosθ;Cos 2θ = cos 2 θ – sin 2 θ = 2 cos 2 θ – 1 = 1 – sin 2 θ;

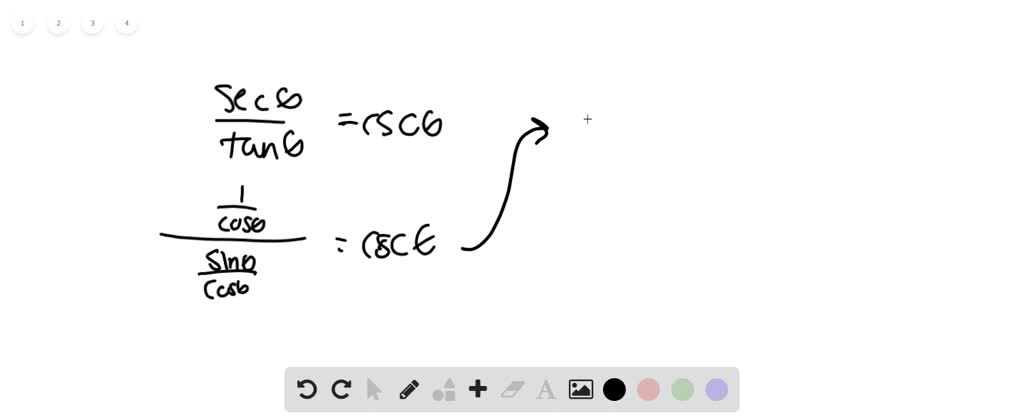
Solved Verify The Following Identities A Sec I Cos I Tan I Sin I B Csc 2 I 1 Tan 2 I Cot 2 I C Cos I I 2 Sin I Please Show Your Work

Tan 2 identities

Tan 2 identities-The Pythagorean Identities $$\begin{array}{c} \cos^2 \theta \sin^2 \theta = 1\\ 1 \tan^2 \theta = \sec^2 \theta\\ 1 \cot^2 \theta = \csc^2 \theta \end{array}$$ Even/Odd Function Identities $$\begin{array}{rcl} \cos (\theta) &=& \phantom{}\cos \theta\\ \sin (\theta) &=& \sin \theta\\ \tan (\theta) &=& \tan \theta \\ \end{array}$$Integral of tan^2(x) How to integrate it step by step!👋 Follow @integralsforyou on Instagram for a daily integral 😉📸 @integralsforyou https//wwwinstag

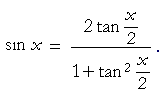
Trigonometric Identities Topics In Trigonometry

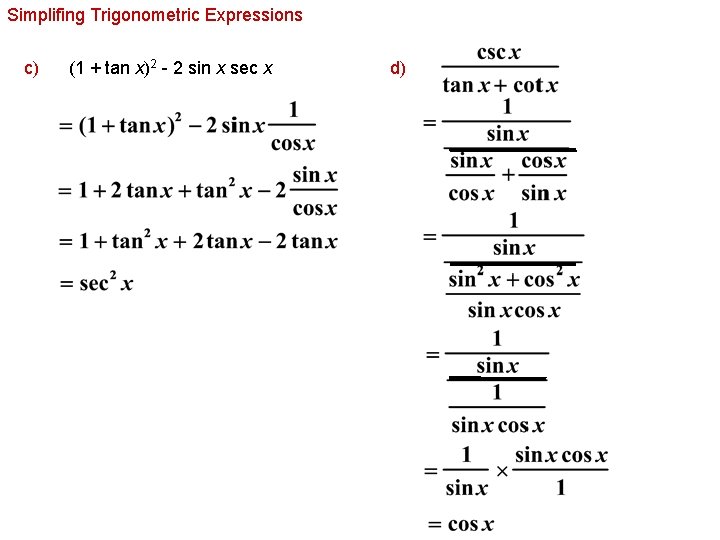
Introduction to Trigonometric Identities and Equations;71 Solving Trigonometric Equations with Identities; 1tan^2x=sec^2x Change to sines and cosines then simplify 1tan^2x=1(sin^2x)/cos^2x =(cos^2xsin^2x)/cos^2x but cos^2xsin^2x=1 we have1tan^2x=1/cos^2x=sec^2x Trigonometry Science

Tan(x)= 1 cot(x) EVEN/ODD IDENTITIES sin(x)=sin(x) cos(x) = cos(x) tan(x)=tan(x) csc(x)=csc(x) sec(x)=sec(x) cot(x)=cot(x) PYTHAGOREAN IDENTITIES cos2(x)sin2(x)=1 tan2(x)1=sec2(x) cot2(x)1=csc2(x) SUM IDENTITIES sin(xy)=sin(x)cos(y)cos(x)sin(y) cos(xy) = cos(x)cos(y)sin(x)sin(y) tan(xy)= tan(x)tan(y) 1tan(x)tan(y) DIFFERENCE IDENTITIESTrigonometry Identity tan^2 (x) 1 = sec^2 (x) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up next in 8The key Pythagorean Trigonometric identity is sin 2 (t) cos 2 (t) = 1 tan 2 (t) 1 = sec 2 (t) 1 cot 2 (t) = csc 2 (t) So, from this recipe, we can infer the equations for different capacities additionally Recall of Pythagoras Theorem You are going to need to rapidly review the three Pythagorean Identities The first Trig Identity of

(x 5)(x − 5) = x 2 − 25 The significance of an identity is that, in calculation, we may replace either member with the other We use an identity to give an expression a more convenient form In calculus and all its applications, the trigonometric identities are of central importance On this page we will present the main identitiesTan (θ/2) = ±√(1 – cosθ)(1 cosθ)Identities to memory, these three will help be sure that our signs are correct, etc 2 Two more easy identities From equation (1) we can generate two more identities First, divide each term in (1) by cos2 t (assuming it is not zero) to obtain tan2 t1 = sec2 t (4) When we divide by sin2 t (again assuming it is not zero) we get 1cot2 t = csc2

Alamo Edu

1

75 Solving Trigonometric Equations;Verify the identity $$(1 \tan x)^2 = \sec ^2 x2 \tan x $$ For this problem, it is best to manipulate the left side $$\begin{align} (1 \tan x)^2 &= 12\tan x76 Modeling with Trigonometric Functions

Sin 2x Formula What Is Sin 2x Formula Examples

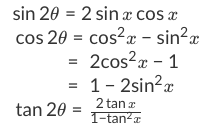
How To Use Double Angle Identities Studypug

Sin (x y) = sin x cos y cos x sin y cos (x y) = cos x cosy sin x sin y tan (x y) = (tan x tan y) / (1 tan x tan y) sin (2x) = 2 sin x cos x cos (2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan (2x) = 2 tan (x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos (2x) cos ^2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 )72 Sum and Difference Identities;1tan2θ=sec2θ 1 tan 2 θ = sec 2 θ The second and third identities can be obtained by manipulating the first The identity 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ is found by rewriting the left side of the equation in terms of sine and cosine Prove 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ

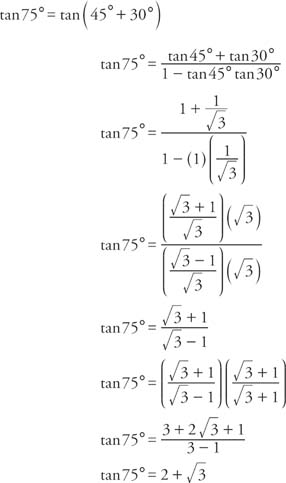
Tangent Identities

Pinkmonkey Com Trigonometry Study Guide 4 4 Tangent Identities

Using double angle identities in trigonometry Identities in math shows us equations that are always true There are many trigonometric identities (Download the Trigonometry identities chart here ), but today we will be focusing on double angle identities, which are named due to the fact that they involve trig functions of double angles such as sin θ \theta θ, cos2 θ \theta θ, and tan2Trigonometric identities are equations involving the trigonometric functions that are true for every value of the variables involved Some of the most commonly used trigonometric identities are derived from the Pythagorean Theorem , like the following sin 2 (142 Trigonometric identities We begin this section by stating about basic trigonometric identites You can refer to books such as the "Handbook of Mathematical Functions", by Abramowitz and Stegun for many moreTo understand them we will organize them into 9 groups and discuss each group

Powers Of Trigonometric Functions

Solved Verify The Identity Tan 2 0 1 Cos 2 1 Tan 2 Chegg Com

List of trigonometric identities 2 Trigonometric functions The primary trigonometric functions are the sine and cosine of an angle These are sometimes abbreviated sin(θ) andcos(θ), respectively, where θ is the angle, but the parentheses around the angle are often omitted, eg, sin θ andcos θ The tangent (tan) of an angle is the ratio of the sine to the cosineFollowing table gives the double angle identities which can be used while solving the equations You can also have #sin 2theta, cos 2theta# expressed in terms of #tan theta # as under #sin 2theta = (2tan theta) / (1 tan^2 theta)# #cos 2theta = (1 tan^2 theta) / (1 tan^2 theta)#18 Verifying Trigonometric Identities In this section, you will learn how to use trigonometric identities to simplify trigonometric expressions Equations such as (x 2)(x 2) = x2 4 or x2 1 x 1 = x 1 are referred to as identities An identity is an equation that is true for all values of xfor which the expressions in the equation are de ned For

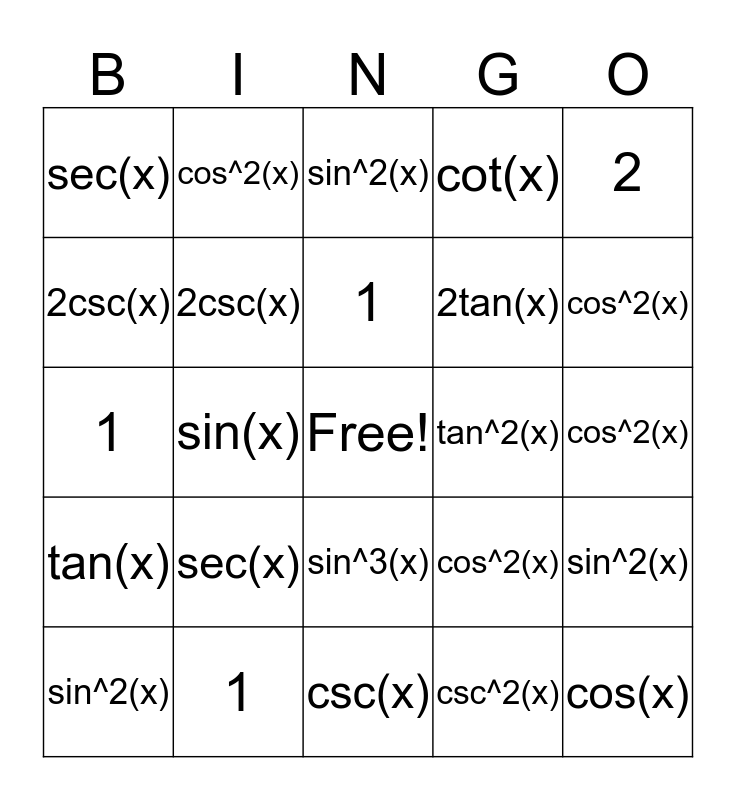
Trig Identities Bingo Card

Get Answer Prove The Given Identity Cos 2 Theta 1 Tan2 Theta 1 Which Transtutors

An example of a trigonometric identity is sin ⁡ 2 θ cos ⁡ 2 θ = 1 \sin^2 \theta \cos^2 \theta = 1 sin2 θcos2 θ = 1 In order to prove trigonometric identities, we generally use other known identities such as Pythagorean identities Prove that ( 1 − sin ⁡ x) ( 1 csc ⁡ x) = cos ⁡ x cot ⁡ x (1 \sin x) (1 \csc x) =\cos x \cot x (1−sinx)(1cscx) = cosxcotxTan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;For most of the problems in this workshop we will be using the trigonometric ratio identities below 1 sin θ cos θ tan θ cot θ csc θ sec θ cot θ tan θ cot θ Guidelines for verifying a Trigonometric Identity 1 Check whether the statement is false • This is easily done on a graphing calculator Graph both sides of the identity and check to see if you get the same picture

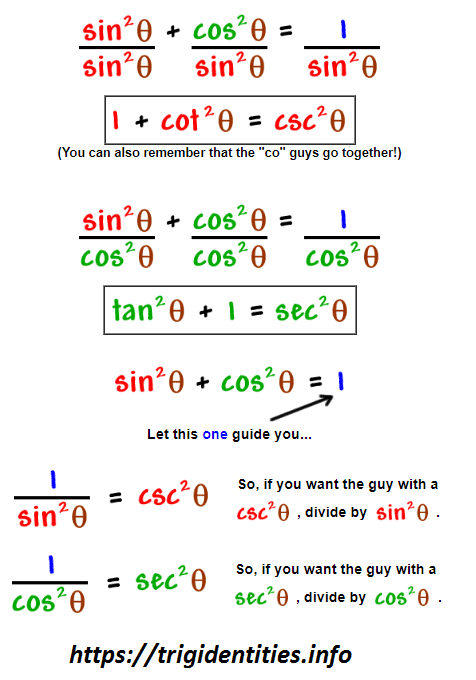
Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

5 1 Fundamental Trig Identities Reciprocal Identities Sin

1 cos ( x) − cos ( x) 1 sin ( x) = tan ( x) Go!74 SumtoProduct and ProducttoSum Formulas;Cos 2x ≠ 2 cos x;

Solved Verify The Following Identities A Sec I Cos I Tan I Sin I B Csc 2 I 1 Tan 2 I Cot 2 I C Cos I I 2 Sin I Please Show Your Work

11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download

Trigonometricidentityprovingcalculator prove \tan^2(x)\sin^2(x)=\tan^2(x)\sin^2(x) enTan 2θ = (2tanθ)/(1 – tan 2 θ) Half Angle Identities If the angles are halved, then the trigonometric identities for sin, cos and tan are sin (θ/2) = ±√(1 – cosθ)/2 cos (θ/2) = ±√(1 cosθ)/2;Tan (2x) = 2 tan (x) / (1 tan 2 (x)) sin 2 (x) = 1/2 1/2 cos (2x) cos 2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 ) cos x cos y = 2 sin ( (xy)/2 ) sin ( (x y)/2 ) Trig Table of Common Angles angle 0

Sum And Difference Identities Video Lessons Examples And Solutions

10 4 Integration Of Powers Of Trigonometric Functions

Get detailed solutions to your math problems with our Proving Trigonometric Identities stepbystep calculator Practice your math skills and learn step by step with our math solver Check out all of our online calculators here! Let's start with the left side since it has more going on Using basic trig identities, we know tan (θ) can be converted to sin (θ)/ cos (θ), which makes everything sines and cosines 1 − c o s ( 2 θ) = ( s i n ( θ) c o s ( θ) ) s i n ( 2 θ) Distribute the right side of the equation 1The key Pythagorean Trigonometric identity are sin 2 (t) cos 2 (t) = 1 tan 2 (t) 1 = sec 2 (t) 1 cot 2 (t) = csc 2 (t) So, from this recipe, we can infer the equations for different capacities additionally Learn more about Pythagoras Trig Identities Dividing through by c 2 gives a 2/ c 2 b 2/ c 2 = c 2/ c 2 This can be simplified to (a/c) 2 (b/c) 2 = 1

Proof Tan 2 1 Sec 2 Youtube

Trigonometric Identities Topics In Trigonometry

Identity tan (2x) Multiple Angle Identities Symbolab Identities Pythagorean Angle Sum/Difference Double Angle Multiple Angle Negative Angle Sum to Product Product to SumTan(x) is an odd function which is symmetric about its origin tan(2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin(2x) to cos(2x) sin(2 x) = 2 sin(x) cos(x) cos(2 x) = (cos(x))^2 – (sin(x))^2 = 1 – 2 (sin(x))^2 = 2 (cos(x))^2 – 1 Proof$\tan^2{\theta} \,=\, \sec^2{\theta}1$ The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula It is also called as the square of tan function identity Introduction The tangent functions are often involved in trigonometric expressions and equations in square form The expressions or equations can be possibly

Tangent Half Angle Formula Wikipedia Republished Wiki 2

Trig Identities For Pre Calculus Dummies

Tan 2x ≠ 2 tan x by Shavana Gonzalez2 2 2 sin22sincos cos2cossin 2cos1 12sin 2tan tan2 1tan qqq qqq q q q q q = ====Degrees to Radians Formulas If x is an angle in degrees and t is an angle in radians then 180 and txt tx x pp p =Þ== Half Angle Formulas (alternate form) (( )) (( )) ( ) ( ) 2 2 2 1cos1 sinsin1cos2 222 1cos1 coscos1cos2 222 1cos 1cos2 tantan 21cos1cos2The half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 Verify the identity Example 6 Verify the identity tan (α/2) = (1 − cos α)/sin α Example 7 Verify the identity tan (α − 2) = sin π/(1 cos α)

How Do You Solve 1 Tan 2x 6 2sec 2x Socratic

Cofunction Identities In Trigonometry With Proof And Examples Owlcation

These identities are known collectively as the tangent halfangle formulae because of the definition of These identities can be useful in calculus for converting rational functions in sine and cosine to functions of t in order to find their antiderivativesPeriodicity of trig functions Sine, cosine, secant, and cosecant have period 2 π while tangent and cotangent have period π Identities for negative angles Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions Ptolemy's identities, the sum and difference formulas for sine and cosineThe Pythagorean Identities are based on the properties of a right triangle cos2θ sin2θ = 1 1 cot2θ = csc2θ 1 tan2θ = sec2θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle tan(− θ)

Lt 14 I Know The Trig Identities Blaine High School Precalculus

Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com

73 DoubleAngle, HalfAngle, and Reduction Formulas; The following are the properties of inverse trigonometric functions Property 1 sin 1 (1/x) = cosec 1 x, for x ≥ 1 or x ≤ 1 cos 1 (1/x) = sec 1 x, for x ≥ 1 or x ≤ 1 tan 1 (1/x) = cot 1 x, for x > 0 Property 2 sin 1 (x) = sin 1 x, for x ∈ 1 , 1 tan 1 (x) = tan 1 x, for x ∈ R cosec 1 (x) = cosec 1 x, forSec 2 t = 1 tan 2 t Identities expressing trig functions in terms of their supplements sin( – t) = sin t cos( – t) = –cos t tan( – t) = tan t Difference formulas for sine and cosine sin (s – t) = sin s cos t – cos s sin t cos (s – t) = cos s cos t sin s sin t Sum, difference, and

Important Trigonometric Identiti

Trigonometric Identities

Tutorial Math Lamar Edu

Trigonometric Identities A Plus Topper

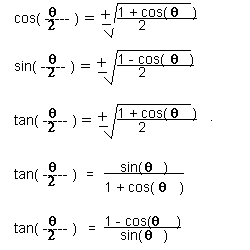
Double And Half Angle Formulas

Summary Of Trigonometric Identities

Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

A Trig Identity

Summary Of Trigonometric Identities

Ppt Analytic Trig Powerpoint Presentation Free Download Id

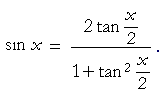
Trigonometric Identities Topics In Trigonometry

Trigonometric Identity Challenge Sin 2 Cos 2x Tan 2x Youtube

How I Remember Trig Identities Part 2 Beyond Solutions

Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube

While You Wait Trigonometric Identities And Equations Section

Sites Math Washington Edu

1

Summary Of Trigonometric Identities

List Of Trigonometric Identities Wikipedia

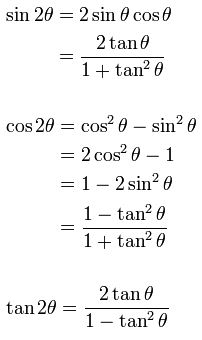
Trigonometric Identities Definition Rules Examples S Sigma Tricks

10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com

Basic Trigonometric Identities And Equations Trigonometric Identities Quotient

Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com

Trig Identities Bingo Card

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

Art Of Problem Solving

How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic

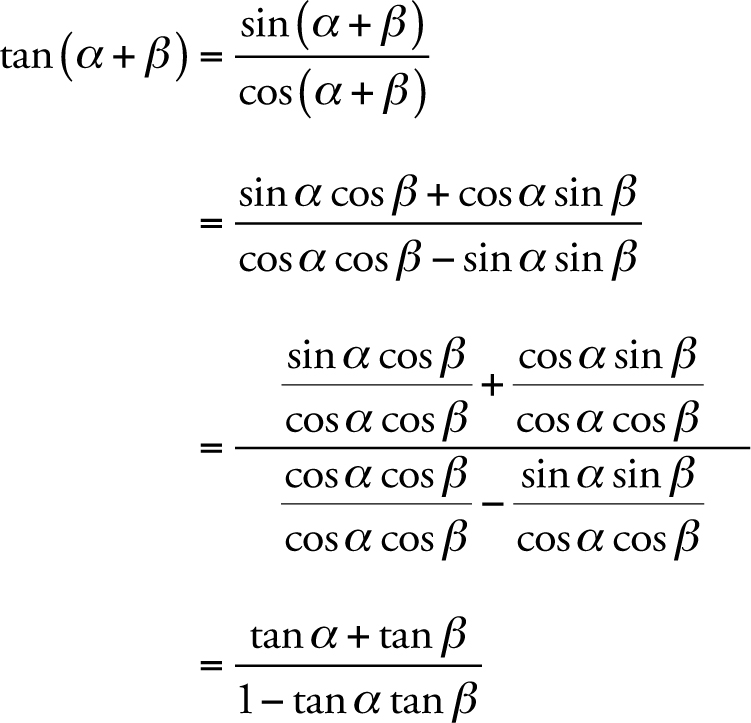
Tangent Identities

How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic

Important Trigonometric Identiti

Reciprocal Identities In Trigonometry With Examples Owlcation

Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube

Tangent Identities

Trig Identities And Formulas Pre Calculus Quiz Quizizz

3

Tangent Half Angle Formula Wikipedia

Brockport Edu

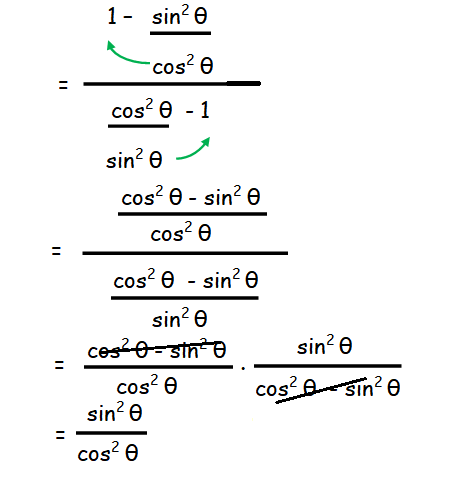
Proving Trigonometric Identities

Understanding Pythagorean Identities Studypug

Ilectureonline

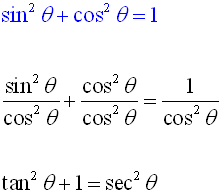
Pythagorean Identities Mathbitsnotebook Ccss Math

Solved Find The Remaining Five Trigonometric Functions Of 0 See Example 1 Sin A 0 In Quadrant Ii 32 Cos 0 0 In Quadrant I 33 Tan 0 Course Hero

Xiwcvukgrtnqdm

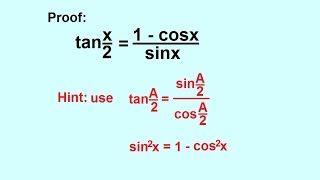
Precalculus Trigonometry Trig Identities 34 Of 57 Proof Half Angle Formula Tan X 2 Youtube

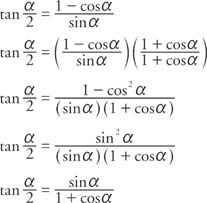
Tangent Identities

Integrate Tan 2x

Tangent Half Angle Formula Wikipedia

Solved Prove The Following Identities Tan 2theta 2 Tan Chegg Com

Right Triangle Trigonometry Is Based Upon Ratios Of

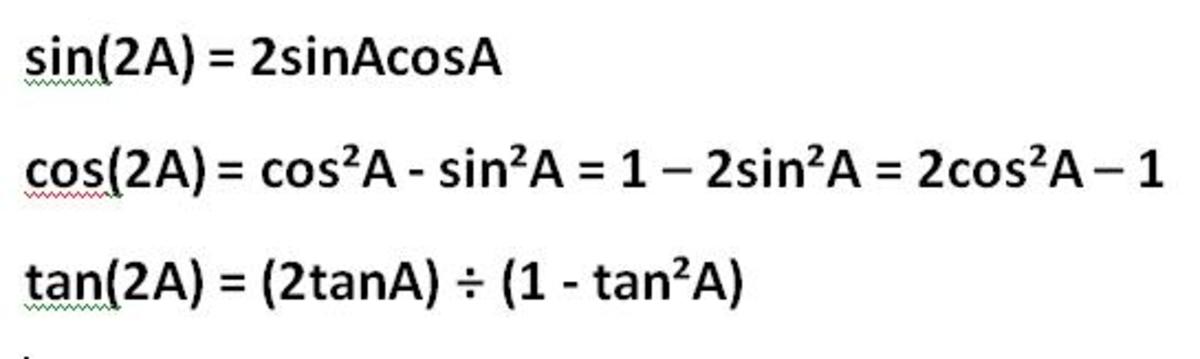
The Double Angle Identities Sin2a Cos2a And Tan 2a Derived From The Trigonometric Addition Formulas Hubpages

Www2 Math Binghamton Edu

Complex And Trigonometric Identities Introduction To Digital Filters

How To Use Double Angle Identities Studypug

Trigonometry Identities

Integrate Sec 2x Method 1

Every Day I M Calculatin I D3 Unit Q Pythagorean Identities

Trigonometry Identities

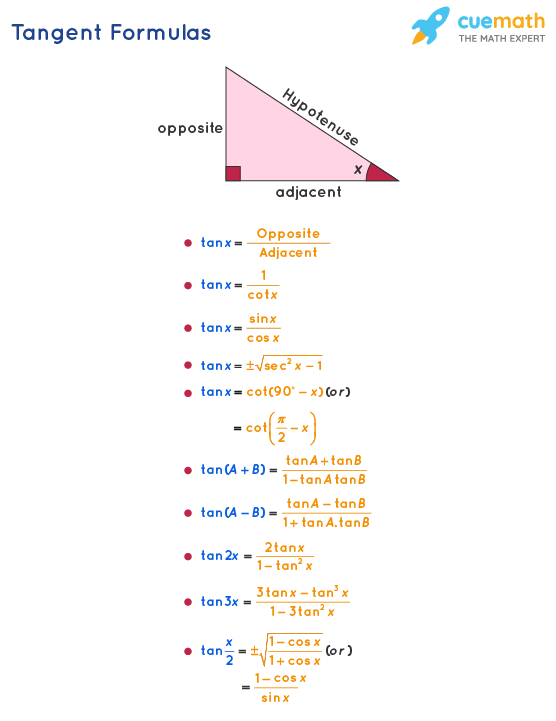
Tangent Formula What Are Tangent Formulas Examples

最も人気のある Tan2 Identity ただの悪魔の画像

Worksheet On Trigonometric Identities Establishing Identities Hints

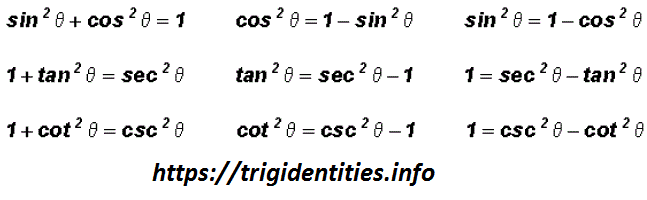
Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

Double Angle Identities Trigonometry Socratic

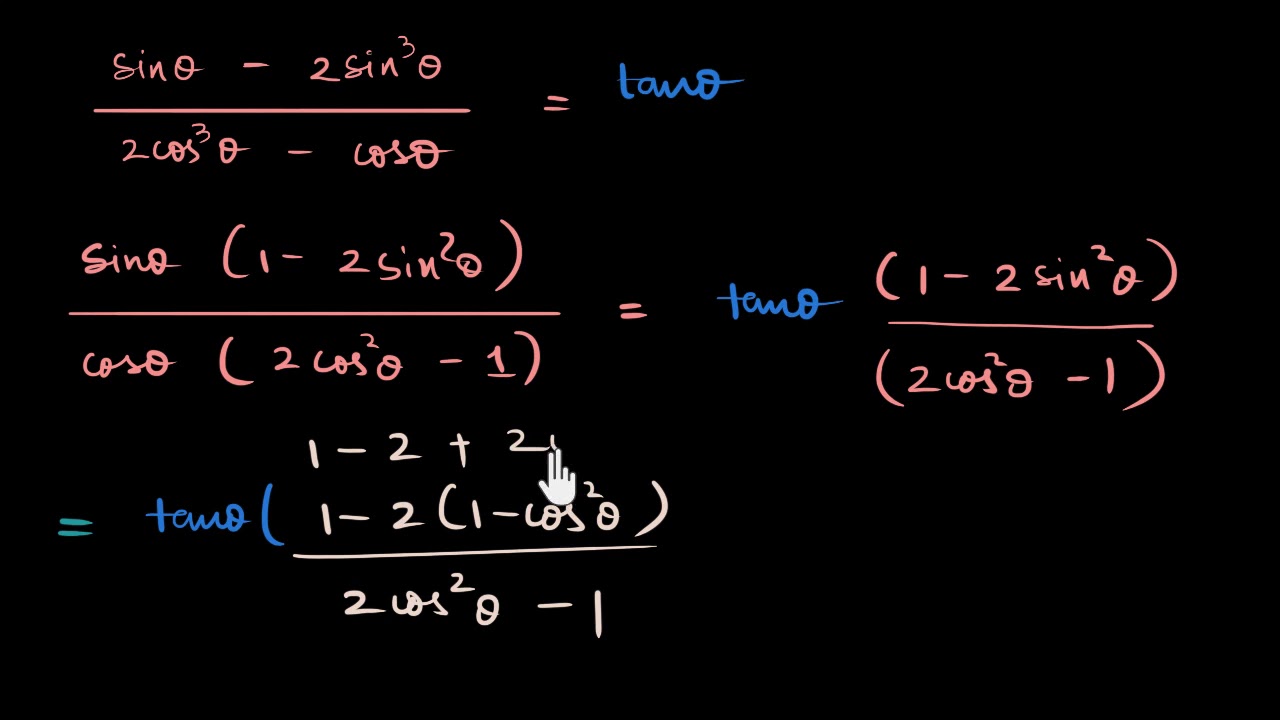
Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy

5 1 5 2 Trigonometric Identities Ppt Download

1

How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic

Pinkmonkey Com Trigonometry Study Guide 4 4 Tangent Identities

What Is The Formula Of Tan2x Quora

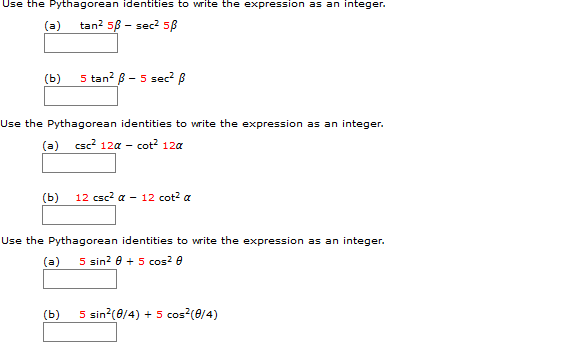
Solved Use The Pythagorean Identities To Write The Chegg Com

上 Tan2x Identity ただの悪魔の画像

Trigonometric Identities

Tangent Half Angle Formula Wikipedia

1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube

Trigonometric Identities A Plus Topper

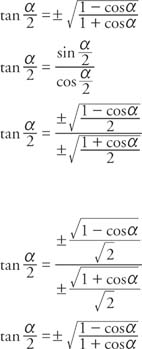
Tangent Identities

Trig Half Angle Identities Trigonometry Half Angle Formulas Derivation

Solved Trig Identities 1 Sin Cos 2 Sin Cos 2 2 2 Tan2 Cos2 Cot2 Sin2 1 3 Sec Course Hero

Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions

Summary Of Trigonometric Identities

Trigonometric Identities List Of Trigonometric Identities Examples

Incoming Term: tan 2 identities, tan 2 x identities, tan 2 theta identities, identities of tan 2,